Dans le petit logo, en bas à droite, une représentation classique du globe terrestre avec l’axe de la Terre incliné de 23°5, une direction qui demeure dirigée vers l’étoile polaire au cours de son orbite annuelle. Ainsi, à six mois d’intervalle, l’hémisphère Nord puis l’hémisphère Sud seront tour à tour les mieux exposés au Soleil.
L’inclinaison de l’axe de la Terre, ou obliquité de l’écliptique, est la différence entre la plus grande hauteur du Soleil, au solstice d’été, et sa hauteur moyenne, aux équinoxes. Les Grecs utilisaient également la double-obliquité qui est l’écart entre sa plus grande hauteur au solstice d’été, et sa plus faible hauteur au solstice d’hiver.
De Thalès et Anaximandre à Callippe de Cyzique les astronomes grecs utilisèrent le gnomon mais leurs mesures de la hauteur du Soleil ne nous sont jamais parvenues. Pythéas le Massaliote, contemporain d’Aristote et de Callippe, est le seul astronome de l’antiquité grecque dont on connaisse une mesure de la hauteur du Soleil par la tangente de l’angle qu’il exprime par le nombre de graduations totales de son gnomon, 120 divisions, et par la longueur de l’ombre au solstice d’été 42 divisions moins 1/5. L’ouvrage de Pythéas, peri okanu, de l’Océan, fut lu et commenté pendant six siècles au moins avant de disparaître à la chute de l’empire romain. Deux mesures astronomiques, celle-ci sur la hauteur du Soleil au solstice d’été, et une autre sur les étoiles voisines du pôle furent miraculeusement sauvées par Strabon, le grand géographe du premier siècle. Cet adversaire féroce ne pardonna jamais à Pythéas d’avoir affirmé que l’on pouvait vivre à la latitude de Thulé ; le réchauffement provoqué par le courant du Gulf stream venait anéantir sa théorie des latitudes climatiques selon laquelle il faisait trop chaud pour vivre à l’équateur, trop froid pour vivre dans les contrées polaires. Aux yeux de Strabon*, Pythéas était le plus menteur des hommes, «il couvre ses mensonges de sa science de l’astronomie et des mathématiques», il avoue encore «en ce qui concerne toutefois l’astronomie et les mathématiques Pythéas semble avoir montré de la capacité». Polybe, historien plus ancien, tout aussi jaloux du fabuleux périple de Pythéas, le concédait aussi : «Il y a lieu de s’étonner qu’il fasse tant de dupes, c’est-à dire qu’il ait tant d’autorité». Eratosthène, Hipparque, Géminos, les astronomes les plus prestigieux, se réfèreront en effet à l’autorité de Pythéas.
Strabon, de - 58 à +23, Géographie, II, V, 41 ; IV,v,5 ; VII,3,1 édition Les Belles Lettres.
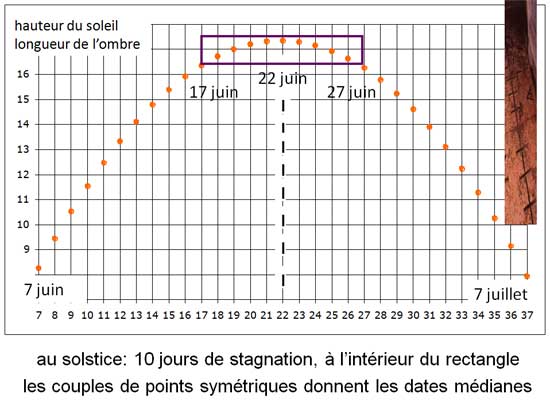
En abscisse nous avons reporté les jours de l’année du 7 juin au 7 juillet, et en ordonnées la hauteur du Soleil au méridien graduée de 5 en 5 minutes d’arc. Ce «choix» de 5’ correspond au mieux que l’on puisse faire même si les graduations de Pythéas 120x5= 600 sub-divisions étaient plus fines. Certes, l’astronome grec Cléomède affirmait que le gnomon de Pythéas était d’une hauteur considérable, mais la limite de la méthode provient du «dégradé» de l’ombre, on ne peut faire mieux que 5’ d’arc mais on y parvient par des mesures répétées au cours de chaque journée et sur une période étalée jusqu’à 15 jours de part et d’autre du solstice, le décalage journalier se comptant alors par plus d’une graduation. A droite, pour mémoire, les repères gradués, en airain, de l’horologium d’Auguste à Rome.
En haut, dans le rectangle, pendant 10 jours, du 17 juin au 27 juin la longueur de l’ombre n’a pas varié de plus de 5’ d’arc, ce n’est pas une surprise car lors du solstice, sol stat, le Soleil stagne à sa hauteur maximum. Mais il existe une méthode assez instinctive, qui consiste à rechercher le point «médian» entre deux positions tout aussi insatisfaisantes l’une que l’autre, mais symétriques, l’une avant le solstice, l’autre après. Une méthode de symétrie, ou «d’équilibrage» comme dans la recherche d’une fréquence radio : on dépasse puis on revient en arrière, et on répète en cherchant le milieu par symétrie. Le résultat est connu en différé.
Ainsi, l’ombre a les mêmes longueurs, les 7 juin et 7 juillet, le 8 juin et le 6 juillet, des couples successifs…. Les dates «médianes» de ces couples symétriques, ici marquées par des «tirets» de couleur noire tracent l’axe vertical de symétrie qui définit la date du solstice désormais connue à 6 heures près, au lieu de 2 à 3 jours à l’origine.
Rappelons que les solstices et équinoxes se produisent à n’importe quelle heure du jour ou de la nuit. Tout astronome consciencieux et prudent effectuera plusieurs relevés, dès le lever du jour jusqu’au coucher, ne serait-ce que pour éviter le risque d’un passage nuageux à l’heure de midi qui viendrait compromettre une séquence d’un mois entier de mesures.
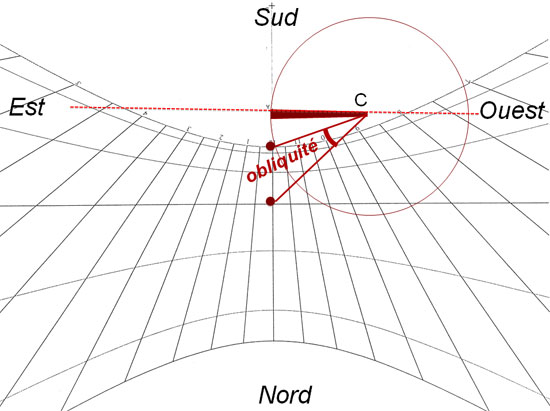
Les textes ne précisent pas comment les astronomes grecs procédaient. J'imagine ici la méthode que Pythèas aurait pu utiliser en rabattant le plan méridien vertical dans le plan de la terrasse et en mesurant l'angle de l'obliquité de l'écliptique sur celle-ci. Pythéas prit de soin à la construction de son instrument de mesure composé d’une terrasse bien horizontale, d’une ligne méridienne graduée, d’un gnomon bien vertical dont la hauteur doit être mesurée avec précision entre sa pointe et un trait gravé à sa base au niveau du sol, et d’un cercle tracé au sol permettant la mesure des angles. Les mesures d’angle étaient alors exprimées en fraction de circonférence, Eratosthène et Hipparque seront les premiers à diviser le cercle en 360°.
Strabon nous dit que le gnomon de Pythéas à Marseille était d’une grande hauteur : « 120 divisions » mais il ne précise pas la valeur de cette unité de base. On doit imaginer que sa hauteur était plus modeste que celle de l’horologium d’Auguste à Rome, instrument de prestige, mais qu’il atteignait la hauteur « optimum » où le dégradé de l’ombre devient perceptible, c’est la « limite ultime de la précision ».
Pour fixer les idées on pourrait supposer un gnomon de 6 mètres de haut (5 cm par division), une terrasse de 30 mètres Sud-Nord par 36 mètres Est-Ouest. Pour mesurer la longueur du gnomon, pour la reporter cette longueur sur la ligne Est-Ouest jusqu’au centre C du futur cercle de mesure, et pour graver les divisions de la ligne méridienne, Pythéas, comme les arpenteurs et bâtisseurs, dut utiliser une toise graduée : imaginons une longueur de 80 cm, soit 16 divisions de 5 cm, facile à graduer uniformément avec un compas, par symétrie, car 16 (2 à la puissance 4) est un sur-multiple de 2.
La verticalité du gnomon était contrôlée par une « groma » constituée de 4 fils à plomb disposés en croix pour les quatre faces. L’horizontalité de la terrasse était vérifiée avec un « corobat », niveau à eau muni de deux pinnules de visée. La ligne est-ouest était tracée le jour de l’équinoxe, jour extraordinaire où l’extrémité de l’ombre décrit une ligne droite. La ligne méridienne était tracée en relevant durant la matinée des positions successives a, b, c, …x, y, z, de l’extrémité de l’ombre, et, l’après-midi, en attendant que la longueur de l’ombre repasse par les mêmes valeurs et en notant les positions z’, y’, x’, …c’, b’, a’. Appelons G l’axe du Gnomon, traçons au compas la bissectrice de aGa’, vérifions ce résultat avec les bissectrices bGb’, cGc’ et effectuons leur moyenne ; il ne reste qu’à graduer cette ligne méridienne Nord-Sud avec la toise.
Sur le graphique, le gros trait rouge en forme d’obélisque, de 120 divisions de longueur, reporte sur le sol la hauteur du gnomon de Pythéas indiquée par Strabon. Son extrémité, le point C est le centre du cercle de mesure des angles. Le rayon de ce cercle, égal à 120 divisions, passe donc par l’axe du gnomon. Ainsi le plan méridien vertical a été rabattu sur la terrasse horizontale.
Les mesures astronomiques peuvent commencer, Les deux points rouges situés sur la ligne méridienne marquent les longueurs de l’ombre mesurées par Pythéas : 41 divisions et 4 cinquièmes au solstice d’été selon Strabon et celle mesurée aux équinoxes 113 divisions. On relie ces deux points au centre C du cercle, cet angle est l’obliquité de l’écliptique ou angle d’inclinaison de l’axe de la Terre.
L’angle étant désormais tracé, on reporte l’arc, ou plutôt la corde, 1 fois, 2 fois, 3 fois…15 fois avant de revenir au point de départ. 1/15e de la circonférence cela fait 24°, c’était la valeur de l’inclinaison de l’axe de la Terre utilisée depuis Thalès jusqu’à Aristote.
Mais les mesures de Pythéas sont plus précises. Il ne trouve pas exactement 15, et il n’y a d’ailleurs aucune raison de trouver un nombre rond. L’angle qu’il mesure est légèrement plus petit 23° 51’ au lieu de 24°. Il lui reste un résidu.

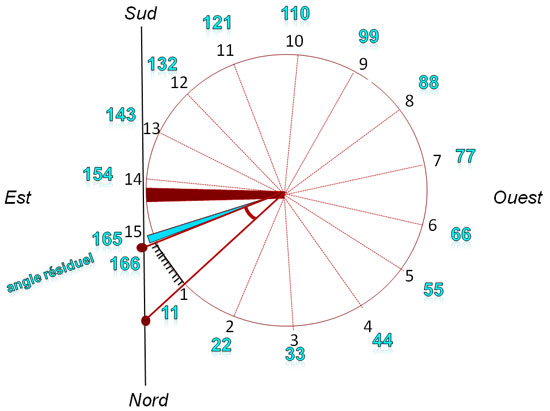
Pythéas prend ce résidu, de couleur turquoise, comme unité de mesure et doit le reporter 11 fois avant de couvrir l’angle de l’obliquité de l’écliptique. Il continue, à grand pas cette fois-ci, afin de couvrir la circonférence entière : 22, 33, 44, 55… (je vous rassure j’ai rencontré des CM2 de la Busserine, quartiers Nord de Marseille, qui connaissaient la table de 11)…jusqu’à 154, 165, plus 1 (le résidu), égal 166…166 fois le résidu pour mesurer la circonférence entière. Pythéas vient d’effectuer une itération après avoir fait une interpolation pour mesurer la date des équinoxes et une extrapolation pour celle des solstices. Résultat, l’angle de l’obliquité est 11/166 soit 23°51’, et la double obliquité est 11/83, une mesure citée par Eratosthène mais dont l’origine remonte sans doute à Pythéas.
Beaucoup attribuent à Erastosthène une mesure de la double-obliquité de l’écliptique, égale à 11/83, qu’il cita dans un de ses textes. Un homme aussi haut placé qu’Eratosthène, philosophe, grammairien, auteur littéraire, chronologiste, géographe, astronome, mathématicien ayant les charges de directeur de la bibliothéque d’Alexandrie et de précepteur de Ptolémée Philopator, pouvait-il consacrer un mois de travail à ces mesures. Eratosthène gagna les surnoms de Bêta et Pentathlos, signifiant qu’il n’était que le second de ces nombreux domaines. S’il avait eu un gnomon de cette qualité, et s’il avait suivi cette procédure d’observation, Eratosthène eut été le mieux placé pour nous livrer ses résultats comme il l’avait fait pour le problème de la moyenne proportionnelle (mésolabe) et pour mesurer la dimension de la Terre, il fit appel à d’autres pour compter le nombre de pas de chameaux entre Syène et Alexandrie et y mesurer la longueur de l’ombre. Le métier de chercheur astrophysicien inclut toujours des mesures de barycentre de profils spectraux, des mesures, qui loin d’être banales, nécessitent des logiciels mathématiques sophistiqués. On peut raisonnablement se ranger aux arguments de Georg Mair* qui, le premier, attribua également à Pythéas la mesure de la double-obliquité de l’écliptique citée par Eratosthène.
Mair Georg, 1904, Pythéas von Massilien und die mathematische geographie, I.Teil, Marburg.


Peu importe Eratosthène, Pythéas ou Callippe, l’essentiel est de comprendre comment dans un texte grec du IVe ou du IIIe siècle avant notre ère, on a pu aboutir à un angle de 11/83, une fraction avec un nombre premier en dénominateur. Complétons notre explication.
Au XVIIe siècle l’astronome Riccioli qui avait découvert la libration lunaire et baptisé les cratères lunaires du nom de grands savants réservant à Hipparque, Eratosthène et Pythéas une place méritée dans ce Panthéon, expliqua qu’Eratosthène divisait les cercles en 83 parties, un nombre premier, de quoi faire frémir la grand mathématicien Gauss qui eut du fil à retordre, tout autant avec 83 qu’avec 17. Cette affirmation irréfléchie de Riccioli lui attira une critique sévère de Delambre* qui à son tour tenta une explication terriblement alambiquée et approximative qui ne fait pas honneur à ce très grand astronome. Selon Delambre, Eratosthène aurait mesuré un angle de 47°40’ soit 47 2/3 sur 360, égal à 143 sur 1080, égal à 11x33 sur 1080, égal à 11 sur (83 +1/3) et d’éliminer ce 1/3 gênant pour aboutir à 11/ 83.
Les grecs ne connaissaient ni les nombres décimaux, ni les fractions, seulement les quantièmes, c’est-à-dire des fractions dont le numérateur est est l’unité, soit une part, une portion. Ainsi pour Hipparque la durée de l’année était 365 jours +1/4 - 1/300 soit 365,247 avec 6 chiffres significatifs. Pour Aristote l’angle de l’obliquité était 1/15e, un quantième, pour Pythéas ce quantième devient 11/166 après une itération de un tour supplémentaire ce n’est pas une véritable fraction mais un quantième itéré du précédent. Archimède, qui vivait un siècle après Pythéas, utilisait aussi cette technique d’itération avec un deuxième tour d’ajustement comme pour la valeur de pi qu'on lui prête égal à 22/7. En fait, si on remonte à la citation originale de Pline, Archimède disait mieux : «est compris entre 3+1/7 et 3+10/71» 1/7 laissait un léger résidu par excès, et 10/71, le quantième dérivé après un deuxième tour, laisse un résidu par défaut.
Delambre Jean-Baptiste, 1817, Histoire de l’Astronomie Ancienne, édition Matthieu
Dès les mesures de Képler et de Gassendi la décroissance de l’obliquité de l’écliptique ne faisait guère de doute mais la communauté des astronomes continua à se montrer réticente. «Si l’axe de la Terre basculait du pôle à l’équateur, cela provoquerait un bouleversement climatique et la vie sur terre deviendrait impossible» argumentait Cassini avec un certain bon sens. Par chance il ne s’agissait pas d’un basculement continu et irréversible mais d’une oscillation sinusoidale de faible amplitude. Au XVIIIe siècle, Euler démontra que la force exercée par Jupiter et Saturne perturbait l’orbite de la Terre, et Laplace calcula que l’inclinaison de l’axe de la Terre oscillait entre 22° et 24°5, en 40 000 ans, et qu’elle était effectivement de 23°46’ au temps de Pythéas, il lui rendait raison.
Cette oscillation de l’inclinaison de l’axe de la Terre entre 22° et 24°5, en 40 000 ans est, avec l’excentricité de l‘orbite terrestre et avec la longitude du périhélie, 126 000 ans (couplée avec la précession 26 000 ans) l’un des 3 paramètres de la théorie astronomique des paléoclimats à l’origine des périodes glaciaires. A lire, Paramètres de Milankovic Wikipedia et Théorie astronomique du climat CNRS.
Laplace Pierre Simon, marquis de, 1799, Exposition du système du Monde, note III, page 491 et Mécanique Céleste, tomeV et tome XIII, édition Gauthiers-Villars.

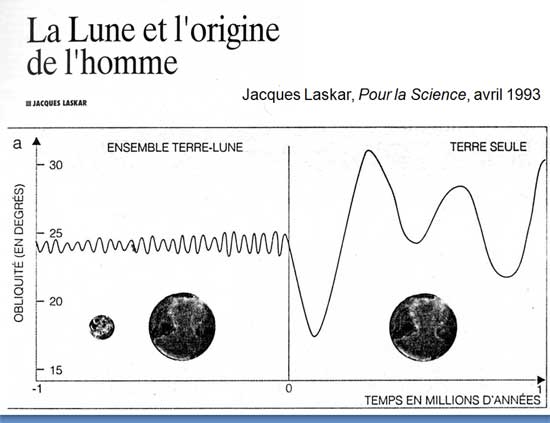
C’est Jacques Laskar, du CNRS et de l’IMCCE Institut de Mécanique Céleste et du Calcul des Ephémérides, meilleur spécialiste international des mouvements planétaires à l’échelle de millions d’années et même de centaine de millions d’années qui nous libére des angoisses de Cassini qui craignait que l’axe de la Terre ne bascule. Jacques Laskar a démontré, par des très gros calculs sur les plus gros ordinateurs américains, que la Lune est notre grand stabilisateur, sans elle la vie n’aurait sans doute pas été possible sur Terre.
La Lune et l’origine de l’homme, tel est le titre et le sujet de l’un de ses articles, Pour la science 1993, où il résume :
«Si la Lune n’existait pas, l’orientation de l’axe de rotation de la Terre ne serait pas stable, et subirait de larges variations chaotiques au cours des âges. Les changements climatiques engendrés par ces variations auraient alors perturbé fortement le développement de la vie organisée».
Le graphique montre le rôle stabilisateur extraordinaire de la Lune; on a vraiment de la chance d’avoir un satellite imposant. Dans le cas de la Terre seule, à droite, l’inclinaison varierait de 17°5 à 31° tandis qu’avec l’ensemble Terre-Lune, à gauche, l’inclinaison oscille de 1,3° autour de sa valeur moyenne 23,3°. Laskar rappelle que cette oscillation minime de +-1,3° de l’obliquité induit tout de même une variation de près de 20% de l’insolation reçue sur Terre à 65° de latitude Nord.
Laskar Jacques, 1993, Pour la Science, n°186, avril 1993.
