Pour Aristarque, au IIIe siècle BC, le Soleil est 180 fois plus volumineux que la Terre,
… et pour Hipparque, au IIe siècle BC, 1880 fois.

«Cette détermination célèbre se trouve dans son Traité sur les grandeurs et les distances du Soleil et de la Lune, où il s’exprime ainsi : à l’instant précis où la Lune est dichotone, ou en quartier, nous, placés sur la Terre, nous nous trouvons dans le plan du cercle qui, sur la Lune, sépare la partie éclairée de la partie obscure ; de sorte que dans le triangle où S est le Soleil, l’angle en L (Lune) est droit».
«Or Aristarque avait mesuré, à ce moment, l’angle en A, ce qui est possible puisque souvent alors le Soleil et la Lune se trouvent simultanément au-dessus de l’horizon. Il l’avait trouvé égal à un quart de cercle moins la trentième partie de l’angle droit, soit 90°-3°=87°». Nous savons aujourd’hui qu’il est de 89°50’.
Aristarque de Samos trouva ainsi que «la distance de la Terre au Soleil est entre 18 fois et 20 fois la distance de la Terre à la Lune». Ce résultat est lui-même 20 fois trop petit, il est vrai, « mais il étendait ainsi le monde bien au delà des limites où l’avaient enfermé jusqu’alors les astronomes et les géomètres ; et pendant 1 800 ans, c’est-à-dire jusqu’à Képler, on n’a pas connu de meilleure méthode pour déterminer la distance de la Terre au Soleil.
Bigourdan Guillaume, 1911, L’astronomie, Evolution des Idées et des Méthodes, édition Flammarion.
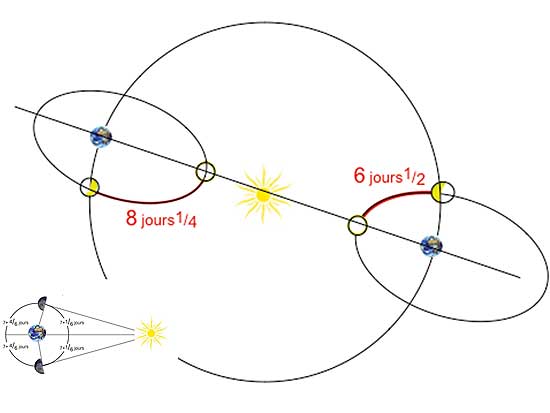
Plusieurs auteurs, conscients à juste titre de la grande imprécision de cette méthode et de la difficulté à déterminer avec précision le moment où l’ombre couvre la moitié de la surface lunaire, se sont interrogés sur une variante de cette méthode ; elle consisterait à décompter le temps qui s’écoule de la Nouvelle Lune au quartier qui devrait être légèrement inférieur au temps qui s’écoule du quartier à la Pleine Lune. Ainsi, pour les mêmes valeurs dans les quadrants au lieu de 90°-3° et 90°+3°on aurait la répartition 7 jours+1/6 et 7 jours + 4/6.
Hélas, c’est sans compter sur l’anomalie lunaire qui condamne cette solution qui continue à se répandre chez les historiens et même certains astrophysiciens. Lors d’une lunaison le premier quartier pourra durer 6 jours ½, mais pour une lunaison décalée de six mois, il durera 8 jours ¼. Une différence énorme, 7 fois plus grande que l’effet du à la distance du Soleil.